DecisionTreeClassifier

Classifier function

Decision Tree Classifier는 데이터 집합에서 다중 클래스 분류를 수행할 수 있는 클래스이다.

다른 분류자와 마찬가지로 Decision Tre Classifier는 훈련 샘플을 고정하는 배열 X(n_샘플, n_특징)와 훈련 샘플에 대한 클래스 레이블을 고정하는 정수 값, 형상(n_샘플, n_특징)의 배열 Y의 두 배열을 입력으로 사용합니다.

1
2
3
4
5

from sklearn import tree
X = [[0, 0], [1, 1]]
Y = [0, 1]
clf = tree.DecisionTreeClassifier()
clf = clf.fit(X, Y)

이제 예측 모델을 만들어 봅시다.

1
2

clf.predict([[2., 2.]])
clf.predict_proba([[2., 2.]])

array([[0., 1.]])

의사결정트리의 분류는 classification과 multiclass 양쪽으로 모두 분류 할 수 있다.

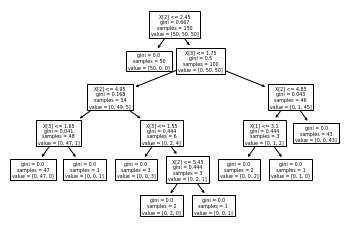
iris dataset을 하용하면, 우리는 아래와 같은 plot_Tree를 만들 수 잇다.

1
2
3
4
5
6
7

from sklearn.datasets import load_iris
from sklearn import tree
iris = load_iris()
x, y = iris.data, iris.target
clf = tree.DecisionTreeClassifier()
clf = clf.fit(x, y)
tree.plot_tree(clf)

[Text(167.4, 199.32, 'X[2] <= 2.45\ngini = 0.667\nsamples = 150\nvalue = [50, 50, 50]'),
 Text(141.64615384615385, 163.07999999999998, 'gini = 0.0\nsamples = 50\nvalue = [50, 0, 0]'),
 Text(193.15384615384616, 163.07999999999998, 'X[3] <= 1.75\ngini = 0.5\nsamples = 100\nvalue = [0, 50, 50]'),
 Text(103.01538461538462, 126.83999999999999, 'X[2] <= 4.95\ngini = 0.168\nsamples = 54\nvalue = [0, 49, 5]'),
 Text(51.50769230769231, 90.6, 'X[3] <= 1.65\ngini = 0.041\nsamples = 48\nvalue = [0, 47, 1]'),
 Text(25.753846153846155, 54.359999999999985, 'gini = 0.0\nsamples = 47\nvalue = [0, 47, 0]'),
 Text(77.26153846153846, 54.359999999999985, 'gini = 0.0\nsamples = 1\nvalue = [0, 0, 1]'),
 Text(154.52307692307693, 90.6, 'X[3] <= 1.55\ngini = 0.444\nsamples = 6\nvalue = [0, 2, 4]'),
 Text(128.76923076923077, 54.359999999999985, 'gini = 0.0\nsamples = 3\nvalue = [0, 0, 3]'),
 Text(180.27692307692308, 54.359999999999985, 'X[2] <= 5.45\ngini = 0.444\nsamples = 3\nvalue = [0, 2, 1]'),
 Text(154.52307692307693, 18.119999999999976, 'gini = 0.0\nsamples = 2\nvalue = [0, 2, 0]'),
 Text(206.03076923076924, 18.119999999999976, 'gini = 0.0\nsamples = 1\nvalue = [0, 0, 1]'),
 Text(283.2923076923077, 126.83999999999999, 'X[2] <= 4.85\ngini = 0.043\nsamples = 46\nvalue = [0, 1, 45]'),
 Text(257.53846153846155, 90.6, 'X[1] <= 3.1\ngini = 0.444\nsamples = 3\nvalue = [0, 1, 2]'),
 Text(231.7846153846154, 54.359999999999985, 'gini = 0.0\nsamples = 2\nvalue = [0, 0, 2]'),
 Text(283.2923076923077, 54.359999999999985, 'gini = 0.0\nsamples = 1\nvalue = [0, 1, 0]'),
 Text(309.04615384615386, 90.6, 'gini = 0.0\nsamples = 43\nvalue = [0, 0, 43]')]

decision tree는 약 20여종의 parameter가 있다.

Parameter

• criterion : 분할 품질을 측정하는 기능 (default : gini)
• splitter : 각 노드에서 분할을 선택하는 데 사용되는 전략 (default : best)
• max_depth : 트리의 최대 깊이 (값이 클수록 모델의 복잡도가 올라간다.)
• min_samples_split : 자식 노드를 분할하는데 필요한 최소 샘플 수 (default : 2)
• min_samples_leaf : 리프 노드에 있어야 할 최소 샘플 수 (default : 1)
• min_weight_fraction_leaf : min_sample_leaf와 같지만 가중치가 부여된 샘플 수에서의 비율
• max_features : 각 노드에서 분할에 사용할 특징의 최대 수
• random_state : 난수 seed 설정
• max_leaf_nodes : 리프 노드의 최대수
• min_impurity_decrease : 최소 불순도
• min_impurity_split : 나무 성장을 멈추기 위한 임계치
• class_weight : 클래스 가중치
• presort : 데이터 정렬 필요 여부

1
2

sklearn.tree.plot_tree(decision_tree, *, max_depth=None, feature_names=None, class_names=None, label='all', filled=False, impurity=True, node_ids=False, proportion=False, rounded=False, precision=3, ax=None, fontsize=None)
tree.plot_tree()

가장 원시적이면서 기본적인 parameter가 있는 decision tree의 parameter를 외우기 보다 지금 어떤 형태로 코드가 들어 가는지에 집중하자.

왜냐하면, 최신의 버전은 decision tree가 아니기 때문.

1
2
3
4
5
6

from sklearn.datasets import load_iris
from sklearn import tree

clf = tree.DecisionTreeClassifier(random_state=0)
iris = load_iris()

machine learning

Decision tree learing

• Decision tree 란

관측값과 목표값을 연결 시켜주는 예측 모델

통계학과 데이터 마이닝, 기계학습에서 예측모델링으로 사용하는 방법

데이터 기능에서 유추된 결정규칙을 학습하여 대상 변수값을 예측 하는 모델을 만들기 위해 사용

종류

• 분류 트리

  • 변수가 유한한 수의 값을 가지는 것, 클래스 출력
  • Leaf node는 클래스 라벨을 나타내고 가지는 클래스 라벨과 관련있는 특징들의 논리 곱을 나타낸다.

• 회귀트리

  • 목표변수가 연속하는 값(일반적으로 실수 )을 가지는 트리
  • 특정 의미를 가지는 실수값을 출력

  의사결정 분석에서 결정트리는 시각적으로 명시적인 방법으로 과정을 보여준다.

결정트리의 학습

• 결정 트리의 학습 : 자료 집합을 적절한 분할기준 또는 분할 테스트에 따라 부분집합들로 나누는 과정

  • 하향식 결정 트리 귀납법 (TDIDT_top-down induction of decision trees)
    • 순환분할 방식으로 나눠진 자료의 부분집합에 재귀적으로 반복됨.
    • 분할로 인해 더이상 새로운 예측값이 추가 되지 않거나 부분집합의 노드가 목표변수와 같은 값을 지닐대 까지 계속됨.

• 데이터 마이닝에서 결정트리

  • 수학 적으로 표현됨

예를 들어 아래와 같은 데이터 마이닝에서의 결정 트리가 있다고 가정 해 보자.

( f{x},Y ) = (x_1, x_2, x_3, ..., x_k, Y)

종속 변수 Y는 분류를 통해 학습하고자 하는 목표 변수이며, 
벡터 x는 {  x_{1}, x_{2}, x_{3} } x_1, x_2, x_3 등의 
입력 변수로 구성된다.

장점

1. 이해하기 쉬우며 시각화 가능
2. data 준비가 거의 필요하지 않음
3. 수치형, 범주형 data를 모두 처리 가능
4. multi-output problems를 다룰 수 있다. 
5. a white box model을 사용 할 수 있다. (bool 가능)
6. 통계 검정을 사용하여 모형을 검증하기 때문에 모델의 신뢰성을 설명할 수 있다.
7. 생성된 데이터가 실제 모형에 의해 가정이 다소 위반되더라도 잘 수행된다.

단점

1. data 일반화가 잘 되지 못하면 복잡한 트리가 만들어짐 (과적합)

    - 가지치기, 리프노드에 필요한 샘플 최소화, 트리 최대깊이 설정 으로 해결 가능
   

2. variation이 작은 경우 의사결정트리가 불안정 할 수 있다.
   • 앙상블(ensemble) 내에서 의사결정 트리 사용으로 해결 가능.
   • 실용적인 의사 결정 트리 학습 알고리즘은 각 노드에서 국소적으로 최적의 의사결정이 이루어지는 그리디 알고리즘과 같은 경험적 알고리즘을 기반으로 한다. 이러한 알고리즘은 전역 최적 의사 결정 트리를 반환한다고 보장할 수 없다.
   • 이는 특징과 샘플이 교체와 함께 무작위로 샘플링되는 앙상블 학습기에서 여러 트리를 훈련시킴으로써 완화될 수 있다.
3. 의사 결정 트리의 예측은 근사치이기 때문에 좋은 추정은 아닐 수 있다.
4. 의사결정 트리의 최적화의 문제는 NP-complete로 잘 알려진 문제이다.
   잘 모르겠다.

• NP-complete

5. XOR, parity or multiplexer problems와 같이 배우기 쉽지 않은 컨셉들 때문에 표현하기 쉽지않다.
6. 학습자가 편향된 트리르르 만들 수 있으므로, 데이터 세트의 균형을 맞춰줘야 한다.

이어지는 posting

• classification
• Regression

Ref.

1. 결정트리학습법/wiki
2. 결정트리 국문
3. Decusuib Trees
4. 1.10.1
5. 1.10.2